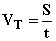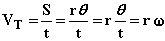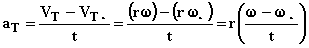سرعت زاویهای و مماسی (خطی)
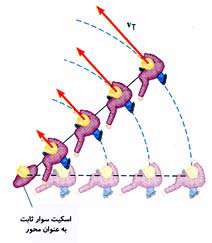
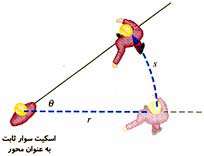
در ورزش اسكی روی یخ یك حركت نمایشی جالب این است كه تعدادی اسكیت باز در یك ردیف مستقیم حول یكی از افراد گروه (كه ثابت است) به چرخش در میآیند. در شكل مقابل این حركت نمایشی نشان داده شده است.
همان طور كه ملاحظه میكنید سرعت افراد در حین حركت یكسان نیست. سرعت هر اسكیت باز مماس بر مسیر حركت میباشد. بنابراین به آن سرعت مماسی نیز میگویند. اندازه و مقدار سرعت مماسی را تندی مماسی مینامند.
به نظر شما چرا در حركت نمایشی بالا، آنكه فاصله اش از مركز چرخش بیشتر است با سختی بیشتری حركت میكند؟
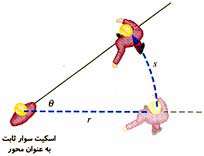
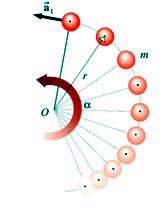
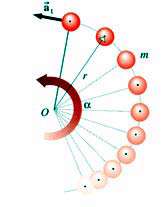
زیرا وی بیش از سایر افراد بایستی حركت كند! بر این اساس سرعت مماسی آن از همه بیشتر است. به كمك شكل زیر میتوان سرعت مماسی را محاسبه نمود.
فرض كنید كه در مدت t ثانیه یكی از اسكیت بازان كه در فاصله r قرار دارد، به اندازه زاویه 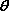 حول محور دوران بچرخد. بدیهی است مسافت پیموده شده بر روی كمان s از رابطه
حول محور دوران بچرخد. بدیهی است مسافت پیموده شده بر روی كمان s از رابطه 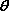 S=r به دست میآید.
S=r به دست میآید.
از طرف دیگر تندی مماسی به عنوان نسبت مسافت پیموده شده روی كمان بر زمان حركت میباشد یعنی:
حال با تركیب دو رابطه اخیر خواهیم داشت:
بنابراین اگر سرعت زاویهای  مشخص باشد آنگاه سرعت مماسی متناسب با شعاع خواهد بود. در اینجا VT و
مشخص باشد آنگاه سرعت مماسی متناسب با شعاع خواهد بود. در اینجا VT و  به ترتیب به اندازه و مقدار سرعت زاویهای و سرعت مماسی اشاره دارند و در آن ها علامت لحاظ نمیشود.
به ترتیب به اندازه و مقدار سرعت زاویهای و سرعت مماسی اشاره دارند و در آن ها علامت لحاظ نمیشود.
اگر یكی از اسكیت بازها سرعت مماسی اش افزایش یابد آنگاه برای حفظ نظم و ردیف لازم است كه سایر افراد نیز (بسته به شعاعشان) سرعتشان را تغییر دهند (  V=r).
V=r).
اما تغییر سرعت به معنی حركت شتابدار است. اگر در لحظه t٠ سرعت مماسی برابر VT٠ و در لحظه t سرعت مماسی VT باشد آنگاه شتاب مماسی بدین گونه تعریف میشود:
اما عبارت داخل پرانتز همان شتاب زاویهای است بنابراین داریم:
این نتیجه نشان میدهد كه برای هر مقدار  شتاب مماسی aT متناسب با شعاع حركت r است. بنابراین اسكیت بازی كه در فاصله دورتر است شتاب مماسی بیشتری را متحمل میشود.
شتاب مماسی aT متناسب با شعاع حركت r است. بنابراین اسكیت بازی كه در فاصله دورتر است شتاب مماسی بیشتری را متحمل میشود.
دقت كنید مقادیر aT و  فقط به اندازه اشاره دارند، بنابراین برای آن ها علامت منظور نمیشود (این موضوع شبیه VT وaT در رابطه
فقط به اندازه اشاره دارند، بنابراین برای آن ها علامت منظور نمیشود (این موضوع شبیه VT وaT در رابطه  VT=r میباشد).
VT=r میباشد).
مرکز یادگیری سایت تبیان - تهیه: محسنی
تنظیم: مریم فروزان کیا